Обучение Коши
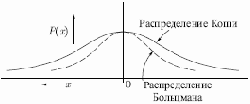
Рис. 7.3.
В этом методе при вычислении величины шага распределение Больцмана заменяется на распределение Коши. Распределение Коши имеет, как показано на рис. 7.3, более длинные "хвосты", увеличивая тем самым вероятность больших шагов. В действительности, распределение Коши имеет бесконечную (неопределенную) дисперсию. С помощью такого простого изменения максимальная скорость уменьшения температуры становится обратно пропорциональной линейной величине, а не логарифму, как для алгоритма обучения Больцмана. Это резко уменьшает время обучения. Зависимость может быть выражена следующим образом:

Распределение Коши имеет вид

где


В данном уравнении



где


Теперь применение метода Монте-Карло становится очень простым. Для нахождения x в этом случае выбирается случайное число из равномерного распределения на открытом интервале

