Использование обучения
Искусственная нейронная сеть обучается с помощью некоторого процесса, модифицирующего ее веса. Если обучение успешно, то предъявление сети множества входных сигналов приводит к появлению желаемого множества выходных сигналов. Имеется два класса обучающих методов: детерминистский и стохастический.
Детерминистский метод обучения шаг за шагом осуществляет процедуру коррекции весов сети, основанную на использовании их текущих значений, а также величин входов, фактических выходов и желаемых выходов. Обучение персептрона является примером подобного детерминистского метода.
Стохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те изменения, которые ведут к улучшениям. Чтобы показать это наглядно, рассмотрим рис. 7.1, на котором изображена типичная сеть, где нейроны соединены с помощью весов. Выход нейрона является здесь взвешенной суммой его входов, которая преобразована с помощью нелинейной функции. Для обучения сети могут быть использованы следующие процедуры:
- Выбрать вес случайным образом и подкорректировать его на небольшое случайное число. Предъявить множество входов и вычислить получающиеся выходы.
- Сравнить эти выходы с желаемыми выходами и вычислить величину разности между ними. Общепринятый метод состоит в нахождении разности между фактическим и желаемым выходами для каждого элемента обучаемой пары, возведение разностей в квадрат и нахождение суммы этих квадратов. Целью обучения является минимизация этой разности, часто называемой целевой функцией.
- Выбрать вес случайным образом и подкорректировать его на небольшое случайное значение. Если коррекция помогает (уменьшает целевую функцию), то сохранить ее, в противном случае вернуться к первоначальному значению веса.
- Повторять шаги с 1 по 3 до тех пор, пока сеть не будет обучена в достаточной степени.
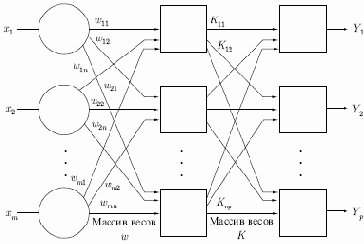
Рис. 7.1.
Этот процесс стремится минимизировать целевую функцию, но может попасть, как в ловушку, в неудачное решение. На рис. 7.2 показано, как это может происходить в системе с единственным весом.
Допустим, что первоначально вес взят равным значению в точке






будут часто посещаться, но то же самое будет верно и для каждой другой точки. Вес будет меняться так резко, что он никогда не установится в желаемом минимуме.
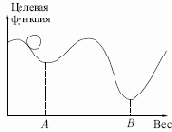
Рис. 7.2.
Таким образом, окончательно шарик остановится в точке глобального минимума, когда амплитуда встряхивания уменьшится до нуля.
Искусственные нейронные сети могут обучаться, по существу, тем же способом при помощи случайной коррекции весов. Вначале делаются большие случайные коррекции с сохранением только тех изменений весов, которые уменьшают целевую функцию. Затем средний размер шага постепенно уменьшается, и глобальный минимум в конце концов достигается.
Эта процедура весьма напоминает отжиг металла, поэтому для ее описания часто используют термин "имитация отжига". В металле, который нагрет до температуры, превышающей его точку плавления, атомы находятся в сильном беспорядочном движении. Как и во всех физических системах, атомы стремятся к состоянию минимума энергии (единому кристаллу, в данном случае), но при высоких температурах энергия атомных движений препятствует этому. В процессе постепенного охлаждения металла возникают все более низкоэнергетические состояния, пока, в конце концов, не будет достигнуто самое малое из возможных состояний, глобальный минимум. В процессе отжига распределение энергетических уровней описывается следующим соотношением:

где




При высоких температурах
