Как обучается многослойный персептрон
Мы сможем лучше понять, как устроен и как обучается многослойный персептрон, если выясним, какие функции он способен моделировать. Вспомним, что уровнем активации элемента называется взвешенная сумма его входов с добавленным к ней пороговым значением. Таким образом, уровень активации представляет собой простую линейную функцию входов. Эта активация затем преобразуется с помощью сигмоидной (имеющей S- образную форму) кривой.
Комбинация линейной функции нескольких переменных и скалярной сигмовидной функции приводит к характерному профилю "сигмовидного склона", который выдает элемент первого промежуточного слоя. На рис. 5.1 соответствующая поверхность изображена в виде функции двух входных переменных. Элемент с большим числом входов выдает многомерный аналог такой поверхности. При изменении весов и порогов меняется и поверхность отклика; может меняться как ориентация всей поверхности, так и крутизна склона — большим значениям весов соответствует более крутой склон. Так, например, если увеличить все веса в два раза, то ориентация не изменится, а наклон будет более крутым. В многослойной сети подобные функции отклика комбинируются друг с другом с помощью последовательного взятия их линейных комбинаций и применения нелинейных функций активации. На рис. 5.2 изображена типичная поверхность отклика для сети с одним промежуточным слоем, состоящим из двух элементов, и одним выходным элементом, для классической задачи "исключающего или". Две разных сигмоидных поверхности объединены в одну поверхность, имеющую форму буквы "U".
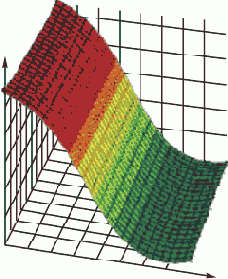
Рис. 5.1.
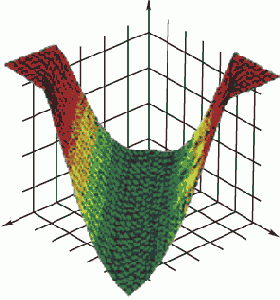
Рис. 5.2.
Перед началом обучения сети весам и порогам случайным образом присваиваются небольшие по величине начальные значения. Тем самым, отклики отдельных элементов сети имеют малый наклон и ориентированы хаотично — фактически они не связаны друг с другом. По мере того, как происходит обучение, поверхности отклика элементов сети вращаются и сдвигаются в нужное положение, а значения весов увеличиваются, поскольку они должны моделировать отдельные участки целевой поверхности отклика.
В задачах классификации выходной элемент должен выдавать сильный сигнал в случае, если данное наблюдение принадлежит к интересующему нас классу, и слабый — в противоположном случае. Иначе говоря, этот элемент должен стремиться смоделировать функцию, равную единице в области пространства объектов, где располагаются объекты из нужного класса, и равную нулю вне этой области. Такая конструкция известна как дискриминантная функция в задачах распознавания. "Идеальная" дискриминантная функция должна иметь плоскую структуру: точки соответствующей поверхности будут располагаться либо на нулевом уровне, либо на высоте "единица".
Если сеть не содержит скрытых элементов, то на выходе она может моделировать только одинарный "сигмовидный склон": точки, находящиеся по одну его сторону, располагаются низко, по другую — высоко. При этом всегда будет существовать область между ними (на склоне), где высота принимает промежуточные значения, но по мере увеличения весов эта область будет сужаться.
Такой сигмовидный склон фактически работает как линейная дискриминантная функция. Точки, лежащие по одну сторону склона, классифицируются как принадлежащие нужному классу, а лежащие по другую сторону — как не принадлежащие. Следовательно, сеть без скрытых слоев может служить классификатором только в линейно-отделимых задачах: когда можно провести линию (или, в случае более высоких размерностей, гиперплоскость), разделяющую точки в пространстве признаков.
Сеть, содержащая один промежуточный слой, строит несколько сигмоидных склонов, — по одному для каждого скрытого элемента, — и затем выходной элемент комбинирует из них "возвышенность". Эта возвышенность получается выпуклой, т.е. не содержащей впадин. При этом в некоторых направлениях она может уходить на бесконечность (как длинный полуостров). Подобная сеть может моделировать большинство реальных задач классификации.
Сеть с двумя промежуточными слоями строит комбинацию из нескольких таких возвышенностей.
Их будет столько, сколько элементов во втором слое, и у каждой из них будет столько сторон, сколько элементов было в первом скрытом слое. После несложного размышления делаем вывод, что, используя достаточное число таких возвышенностей, можно воспроизвести поверхность любой формы — в том числе с впадинами и вогнутостями.
Как следствие наших рассмотрений мы получаем, что, теоретически, для моделирования любой задачи достаточно многослойного персептрона с двумя промежуточными слоями (в точной формулировке этот результат известен как теорема Колмогорова). При этом может оказаться, что для решения некоторой конкретной задачи будет более простой и удобной сеть с еще большим числом слоев. Однако для решения большинства практических задач достаточно всего одного промежуточного слоя, два слоя применяются как резерв в особых случаях, а сети с тремя слоями практически не применяются.
В задачах классификации очень важно понять, как следует интерпретировать те точки, которые попали на склон или лежат близко от него. Стандартный подход заключается в том, чтобы для пороговых значений установить некоторые доверительные пределы (принятия или отвержения), которые должны быть достигнуты, чтобы данный элемент считался "принявшим решение". Например, если установлены пороги принятия/отвержения 0,95/0.05, то при уровне выходного сигнала выше 0,95 элемент считается активным, при уровне ниже 0,05 — неактивным, а в промежутке — "неопределенным". Имеется и более тонкий (и, вероятно, более полезный) способ интерпретировать уровни выходного сигнала: считать их вероятностями. В этом случае сеть выдает несколько большую информацию, чем просто "да/нет": она сообщает нам, насколько (в некотором формальном смысле) мы можем доверять ее решению. При этом, однако, вероятностная интерпретация обоснована только в том случае, если выполняются определенные предположения о распределении исходных данных (конкретно, что данные являются выборкой из некоторого распределения, принадлежащего к семейству экспоненциальных распределений).Здесь, как и ранее, может быть принято решение по классификации, но, кроме того, вероятностная интерпретация позволяет ввести концепцию "решения с минимальными затратами".